レイ・フロンティア株式会社のデータアナリストの齋藤です。最近、食事がうどんばかりです。
本記事では、機械学習において盛んに応用され、深層学習のライブラリ tensorflow の名前の由来にもなっているテンソルについて述べます。機械学習においては、たとえば映画館の顧客について、「顧客の好み」「映画の種類」「放映された季節」など複数の"次元"を持つデータを多重配列として表現し、その類似度を求めるということが行われます。実際の計算処理のなかではテンソルは単なる多重配列として表現されますし、そのような理解で十分とする解説記事も多くあります。その一方で、テンソルの定義が気になって調べてみると難しい数学の説明ばかりでわけが分からなかった……という経験をした方も多いと思われます。そこで、本記事ではテンソルの数学的な定義と多重配列との関連について、その"気持ち"の部分をわかりやすく解説することを目指しました。少しでも納得に近づければ幸いです。
テンソルを導入するモチベーション
テンソル(tensor)という言葉の由来は、弾性学における"引っ張る力"を意味するテンション(tension)といわれています。現在テンションの概念は、材料力学において、物体の内部に加えられる力の大きさと方向を表し、物体の変形・破壊などを調べるのに使われる応力テンソル(stress tensor)に継承されています。まずは、この応力テンソルによって、テンソルの概念が自然に現れる様子を見ていきます。
応力テンソル
物体(連続体)の点\(r\)で、単位法線ベクトル\({\bf n}\)と面積\(\delta S\)をもつ面を考えます。この面を通じて、面の表側(\(r\)が向いている側)から裏側へもたらされる力を\(T({\bf n})\delta S\)と書くことにします。\(T({\bf n})\)は点\(r\)においてその面に作用する、単位面積あたりの力を表します。これを応力といいます。
ここで、物体を微小な四面体の集まりとして近似することを考え、面と接している四面体にはたらく力を考えます。ここで、四面体は3つの座標軸に垂直な3つの面をもっているとします。
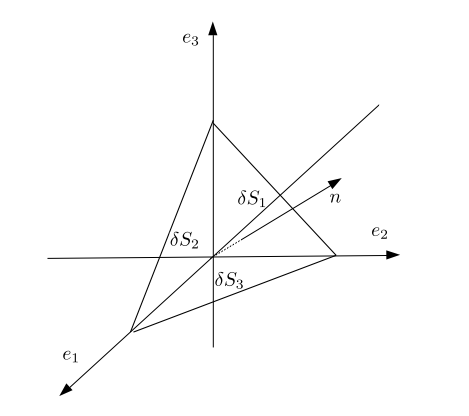
この四面体にはたらく力は慣性力・外力・面積力の3種類ありますが、そのうち慣性力と外力は体積力であり、四面体の長さのスケール\(\delta l\)の3乗のオーダーを持ちます。面積力は2乗のオーダーなので、これらの力は四面体が十分に小さければ無視しても構いません。このとき、四面体に作用する面積力がつり合うと考えて、つり合いの式$$T({\bf n})\delta S + \sum_{j=1}^3 T(-{\bf e_j})\delta S_j = 0$$を得ます。ここで\(\delta S, \delta S_j\)はそれぞれの面の微小面積であり、\({\bf e}_j\)は\(x_j\)軸方向の単位ベクトルをさします。
\(\delta S_j = ({\bf n} \cdot {\bf e}_j ) \delta S\)であることから、$$T({\bf n}) = \sum_{j = 1}^3 T({\bf e}_j)({\bf n} \cdot {\bf e}_j )$$ となるので、3つの座標軸に垂直な面に作用する応力\(T({\bf e}_j)\ (j = 1,2,3)\)を知ることができれば、任意の面に作用する応力\(T({\bf e})\)を知ることができます。
ベクトル\(T\)の第\(i\)成分を\(T_i\)と書いたうえで、$$\sigma _{ij} := T_i({\bf e}_j)$$と定義すれば、\({\bf n} \cdot {\bf e}_j = {\bf n}_j\)より、$$T_i({\bf n}) = \sigma_{ij} {\bf n}_j$$と書けます。この9個の量\(\sigma_{ij}\)を成分とする量を応力テンソルと呼びます。
応力テンソルは9次元ベクトル空間のベクトルですが、力や位置のように"まっすぐ縦に数を並べた"量ではなく、\(i\)と\(j\)という2つのパラメータによって行列のように"2次元的に並べた"量として表現されます。その意味で、応力テンソルは通常のベクトルとは区別されるべき存在といえます。このような、成分を2次元的に並べられる量は2階のテンソルと呼ばれます。同様に、3,4,...次元的に並べられる量は3,4,...階のテンソルと言うことができます。
応力テンソルなど、物理学に現れるテンソルは、上にみた例のように多次元的に並べた時の各成分\(\sigma_{ij}\)のことをさして言うのが通例です。一方、近年応用の目覚ましい機械学習におけるテンソルは多次元的に並べられたデータの集まりであり、数学におけるテンソル積は普遍性と呼ばれるあるベクトル空間の性質から抽象的に定義される量です。このように学問領域によって言葉の使い方にばらつきがあることが、テンソルの定義の理解の妨げになっているのではないかと邪推しています。
テンソル積の定義
ここでは、数学的なテンソル積の定義を紹介することになります。しかし困ったことに、数学におけるテンソル積の定義にも異なる流儀が存在するのです(もちろん、どの定義を用いても結局は同じものが作られます)。本記事では、ベクトル空間のテンソル積の3種類の定義を紹介します。定理の証明を詳しく追いたい方は、参考文献に挙げた線形代数の本を参照してください。とくに[5]は本記事の執筆におおいに参考にしています。
方法1: 普遍性による定義: 基底を用いる
\(V,W\)を線形空間とします。係数体は何でもいいですが、\(\mathbb{R}\)や\(\mathbb{C}\)だと思って差し支えません。直積\(V\times W\)上の双線形写像の集合\(\mathscr{L}(V,W;U)\)を考えます。ここで、像の空間\(U\)を色々変えてみることを考えます。そうすると、\(U\)によらない特別な線形空間\(U_0\)と特別な双線形写像\(\iota : V \times W \to U_0\)が存在することが知られています。どういう風に特別なのかというと、\(U\)と、双線形写像\(\Phi:V \times W \to U\)をどのようにとったとしても、\(\iota\)によって\(\Phi\)は"線形化"されてしまうのです! この"双線形写像の線形化"という側面は、線形空間におけるテンソル積では本質的です。
そのような\(\iota\)を実際に作ってみましょう。\(V,W\)をそれぞれ\(n,m\)次元線形空間とし、それらの基底を1つずつ選んでそれぞれ\(\langle e_1,e_2,\dots,e_n\rangle , \langle f_1,f_2,\dots,f_m\rangle\)とおきます。また、\(U_0\)を\(mn\)次元線形空間として、\(\langle g_{11},g_{12},\dots, g_{1m},g_{21},g_{22},\dots, g_{2m},\dots, g_{n1},g_{n2},\dots, g_{nm}\rangle\)をその基底とします(\(n\)行\(m\)列に並べています)。そして、写像\(\iota: V\times W \to U_0\)を$$\begin{align}&V \ni v = \sum_i \alpha_i e_i,\ W \ni w = \sum_j \beta_j f_j\ (\alpha_i, \beta_j \in K)\ に対して\\& \iota(v,w) = \sum_{i,j} \alpha_i \beta_j g_{ij} \end{align}$$ によって定義します。
このとき、\((U_0,\iota)\)に関して次が成り立ちます:
(1)\((U_0,\iota)\)に関して以下が成立する:
\((\otimes)\) \(^\forall \Phi \in \mathscr{L}(V,W;U)\)に対して、\(\Phi=F\circ \iota\)となる線形写像\(F: U_0 \to U\)がただ一つ存在する。
(2) (1)の性質をもつ\((U_0,\iota)\)は次の意味で一意的である: 線形空間と双線形写像の組\((U_0,\iota), (U_0^\prime,\iota^\prime)\)がともに(1)の性質をもつならば、線形同相写像\(F_0: U_0\to U_0^\prime\)であって\(F_0\circ \iota = \iota^\prime\)となるものがただ一つ存在する。
重要なのは性質\((\otimes)\)です。感覚的に述べると、任意の(任意の空間への!)双線形写像\(V\times W \to U\)は、写像\(\iota\)を通すことによって線形写像\(U_0 \to U\)へと"線形化"することができるのです。このような、\(V\)と\(W\)のみによって定まり、ある意味で任意の\(U\)と\(\mathscr{L}(V,W;U)\)を統制する性質のことは、普遍性(universality)とよばれています。"線形化"写像\(\iota\)を改めて\(\otimes\)、\(U_0\)を\(V\otimes W\)と書き、\(V\otimes W\)をベクトル空間\(V,W\)のテンソル積、\(\otimes\)をテンソル積の標準写像と呼びます。また、ベクトル\(v\in V,w \in W\)について\(\otimes(v,w)\)を\(v\otimes w\)と表記します。これで、ひとまず我々が求めていたテンソル積の定義が手に入りました。
テンソル積は以下の性質をもちます:
\(\alpha, \beta \in K,\ v,v_1,v_2 \in V,\ w,w_1,w_2 \in W\)として、$$\begin{align}(\alpha v_1 + \beta v_2)\otimes w = \alpha (v_1 \otimes w) + \beta (v_2 \otimes w)\\ v\otimes (\alpha w_1 + \beta w_2) = \alpha (v \otimes w_1) + \beta (v \otimes w_2)\end{align}$$
方法2: 普遍性による定義: 基底を用いない
方法1では具体的に\(V,W,U\)の基底を1つとることによって標準写像を定義しましたが、線形空間の双対空間を用いれば、基底をとることなしにテンソル積を構成することもできます。
\(V,W\)の双対空間をそれぞれ\(V^\ast, W^\ast\)とし、$$U_0 = \mathscr{L}(V^\ast, W^\ast;K)$$とおきます。与えられた\((u,w) \in V\times W\)に対して、対応$$V^\ast \times W^\ast \ni (\phi, \psi) \mapsto \phi(v)\psi(w) \in K$$は\(V^\ast \times W^\ast\)から\(K\)への双線形写像を成すのでこれを\(\iota(u,w)\)とすればOKです。あとは方法1と同様にテンソル積を定義して、定理1や命題2を確かめることができます。
方法3: 商空間を用いる定義
3つめの方法は、線型空間の商空間を用いるものです。この流儀の定義は一見すると分かりにくいですが、重要なのはあくまで普遍性と双線形性であって、構成そのものを気にする必要はありません。
直積集合\(V\times W\)について、以下のような線形空間が定義できます:$$\mathscr{V}(V\times W) = \left\{ \sum_{(v,w) \in V\times W} \alpha(v,w) e(v,w) \middle| \alpha(v,w)\not=0となる(v,w)は高々有限個 \right\}$$ここで、\(\alpha(v,w) \in K\)であり、\(e(v,w)\)は\( (v,w)\in V\times W\)に対応する"もの"です。多項式\(\sum_i \alpha_i X^i\)の不定元のようなものだと思っておけばよいでしょう。
次に、\(\mathscr{V}(V\times W)\)の部分空間であって、次の形の元全体によって生成されるものを\(X\)とおきます:$$\left\{\begin{align} &e(v_1+v_2,w) - e(v_1,w) - e(v_2,w)\\ &e(v,w_1+w_2) - e(v,w_1) - e(v,w_2)\\ &e(\alpha v,w) - \alpha e(v,w)\\ &e(v,\alpha w) - \alpha e(v,w)\quad (v_1,v_2,v \in V,\ w_1,w_2,w \in W,\ \alpha \in K)\end{align}\right.$$商線形空間\(\mathscr{V}(V\times W)/X\)を\(U_1\)とおきます。また、\(\mathscr{V}(V\times W)\)から\(U_1\)への自然な射影を\(\pi\)とします。\(X\)の定義から、$$\pi (e(v_1+v_2,w)) - \pi (e(v_1,w)) - \pi (e(v_2,w)) = 0$$などが成り立ちます。ここから双線形性の雰囲気が何となく感じ取れるのではないでしょうか。
そして、写像\(e: V\times W \to \mathscr{V} (V\times W)\)と\(\pi\)の合成写像を\(\iota_1\)とおくと、次が成り立ちます:
\(U_1,\iota_1\)は(方法1,2で定義した)テンソル積\(V\otimes W\)に同型である。
高階テンソル
上で定義したテンソル積は2つの線形空間のある種の積でした。よってこれを2階のテンソルと呼びます。
テンソル積と線形空間のテンソル積を考えることも可能です。3つの線形空間\(V_1,V_2,V_3\)について、$$(V_1\otimes V_2)\otimes V_3 \cong V_1\otimes (V_2\otimes V_3)$$が成り立ちます。よって括弧の順番を気にすることなく\(V_1\otimes V_2\otimes V_3\)と書いてOKです。これを3つの線形空間のテンソル積、すなわち3階のテンソル積と呼びます。同様に、\(n\)個の線形空間\(V_1,V_2,\dots, V_n\)のテンソル積\(V_1\otimes V_2\otimes \cdots \otimes V_n\)を\(n\)階のテンソルと呼びます。\(n\)階のテンソルに関しても2階の場合と同様、\(n\)重の多重線形写像を"線形化"するという意味での普遍性と、\(n\)重線形性をもつことが確認できます。
スカラーは0階のテンソル、普通のベクトルは1階のテンソルと呼ばれます。データを"\(n\)次元に並べられる"ときに\(n\)階テンソル、ということになります。
多重配列としてのテンソル
さて、もう一つの目的であったテンソル積と多重配列との関係ですが、いったん定義を与えてしまえば簡単です。線形空間のテンソル積を方法1によって与えることにして、\(n\)個の線形空間\(V_1,V_2,\dots, V_n\)の基底を\(\langle e_{i,1},e_{i,2},\dots e_{i,m_i} \rangle,\ i=1,2,\dots, n\)とおきます。\(n\)階のテンソル\(V_1\otimes V_2\otimes \cdots \otimes V_n\)の元を、基底を用いて$$\sum_{j_1,j_2,\dots, j_n}\alpha(j_1,j_2,\dots, j_n) e_{1,j_i}\otimes e_{2,j_2}\otimes \cdots \otimes e_{n,j_n},\quad \alpha(j_1,j_2,\dots, j_n) \in K$$と書いたとき、係数\(\alpha(j_1,j_2,\dots, j_n)\)を\(n\)次元配列の成分\(\alpha[j_1][j_2]\dots [j_n]\)に対応させればOKです。プログラミングの世界における多重配列としてのテンソルの背景には、このような"普遍性(双線形写像の線形化)・双線形性"という興味深い構造が隠されていたのでした。
参考文献
[1] 石黒勝彦, 林浩平 (2016), "関係データ学習", 講談社
[2] 河合佑太, "気象力学を学ぶ上での基礎知識", http://epa.scitec.kobe-u.ac.jp/~ykawai/project/meteo_basic/
[3] 斎藤毅 (2007), "線形代数の世界", 東京大学出版会
[4] 佐武一郎 (1958), "線型代数学", 裳華房
[5] 横沼健雄 (1977), "テンソル空間と外積代数", 岩波書店