- 1. 三陸鉄道ってどんな列車?
- 2. 主要駅と観光スポット
- 3.駅周辺と観光地の滞在から魅力に迫る
- 4. 調査元データ
- 5. 今年で開業40周年を迎える三陸鉄道
- 6. 今回のまとめと今後の展望
- お知らせ
1. 三陸鉄道ってどんな列車?
岩手県の海岸沿いを走る地元住民の足として欠かせない三陸鉄道(通称:さんてつ)をご存じでしょうか?
東日本大震災や台風など自然災害などを乗り越え、何度も立ち上がり、走り続けてきた岩手県の三陸鉄道。 2019年には旧JR山田線から宮古〜釜石間が移管され、第三セクターとしては日本最長の、全長163kmとなりました。
三陸鉄道リアス線は「盛駅」~「久慈駅」間で南北に縦貫するような形で繋がっており、全駅が岩手県に位置しています。
座席がこたつ仕様で、太平洋を眺めながら三陸の海の幸が詰まったお弁当を楽しむことができる冬の名物「こたつ列車」のほか、季節ごとのイベントを行っているローカル列車で、地元住民だけでなく観光客からも愛されています。
三陸鉄道は2024年4月1日に開業40周年を迎え様々なキャンペーンを実施しており、今年はさらに盛り上がりを見せている注目の鉄道です。
今回はそんな三陸鉄道の主要駅にフォーカスし、弊社独自に収集している人流データを使って、岩手県の魅力と駅周辺の滞在傾向を見てみました!
自然が堪能できる旅先をお探しの方や列車旅にご興味のある方もぜひご覧ください。
2. 主要駅と観光スポット
三陸鉄道リアス線の起点「盛駅」、終点「久慈駅」のほか、別の路線への乗り換えに利用する「宮古駅」「釜石駅」など主要駅はいくつかありますが、その他にも撮影スポットとして有名であったり、駅舎が特徴的など主要駅以外にも魅力的な駅はあります。そこで今回は以下の8駅に絞って観光地をご紹介します。
盛(さかり)駅

大船渡市にある、三陸鉄道起点となる盛駅。
椿の里とも言われています。「長谷寺(ちょうこくじ)」「天神山(てんじんやま)公園」「長安寺(ちょうあんじ)」などがあります。
釜石(かまいし)駅

桜の名所として人気のある「薬師公園」があります。『JR釜石線 花巻駅』行きの乗り換えに利用する駅であり、鉄と魚とラグビーの街とも言われています。駅前広場の「釜石復興の鐘」は、東日本大震災の犠牲者の鎮魂と復興への祈りが込められ全国の支援者の協力で建てられました。その他にも「イオンタウン釜石店」「釜石市民ホールTETTO」など大きい施設がある駅です。
大槌(おおつち)駅

ひょうたん型の駅舎は蓬莱島を模したデザインになっています。大槌町に所在する「蓬莱島」は、ひょうたん島の愛称で大槌町の人々に親しまれています。
宮古(みやこ)駅

『JR山田線 盛岡駅』行きの乗り換えに利用する駅であり、駅前の観光案内所等で最東端訪問証明書が購入できます。観光スポットは、遊覧船「うみねこ丸」での周遊や「浄土ヶ浜」など。休憩スペースで買ったお刺身が食べられる「宮古市魚菜市場」などもあります。
普代(ふだい)駅

道の駅を併設しているので売店や、休憩スペースがあります。お土産の購入に立ち寄るのもいいですね。昆布の粉末を練りこんだ「こんぶソフトクリーム」は塩気があり濃厚ミルクに合う一品だそうです。
堀内(ほりない)駅

ドラマのロケ地にも使用された駅です。リアス線で一番の車窓を楽しめるスポットとも言われています。
堀内駅と白井海岸駅の間にあり、太平洋を一望できる「大沢橋梁」は長さ156m、高さ30mあり、路線一番の景勝地のようです。親潮と黒潮がぶつかることで豊かな海の幸に恵まれ世界三大漁場に数えられています。そしてもうひとつ、野田玉川駅と堀内駅の間には、長さ302m、高さ33mの「安家川(あっかがわ)橋梁」があり、秋にはたくさんの鮭が川を遡上する光景を見ることができるそうです。
どちらもよく見えるように、日中帯には乗客が撮影できるように橋の上で列車が一時停車、または徐行するので観光客も安心して写真に収めることができます。
陸中野田(りくちゅうのだ)駅

三陸鉄道と村営・市民バスの駅で、観光物産館、産直施設を併設している「道の駅のだ」があります。「観光物産館ぱあぷる」の名称は十府ケ浦(とふがうら)海岸の「小豆砂」が由来だそうです。道の駅で購入できる「のだ塩ソフト」が有名で、他にはお魚センターや、のんちゃんパークと呼ばれている十府ヶ浦公園があります。
久慈(くじ)駅

リアス線の最北端に位置し、三陸鉄道終点となる久慈駅。
ドラマの舞台モデルとなり、ドラマ内ではロケ地として使われた「小袖海岸」があります。街中にはドラマにまつわるイラストや展示がたくさんあります。
3.駅周辺と観光地の滞在から魅力に迫る
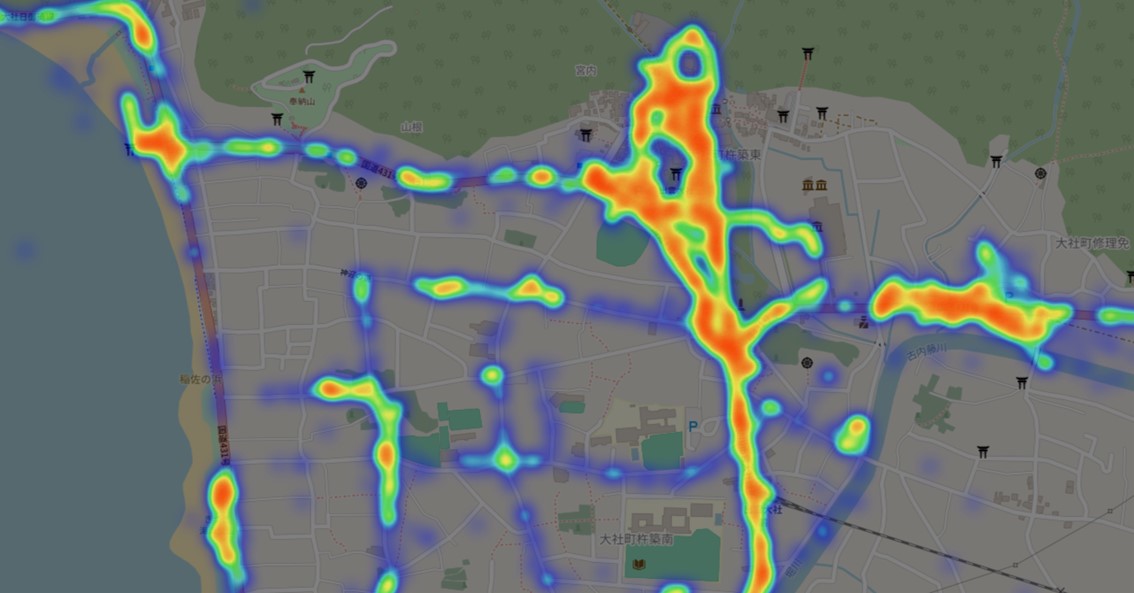
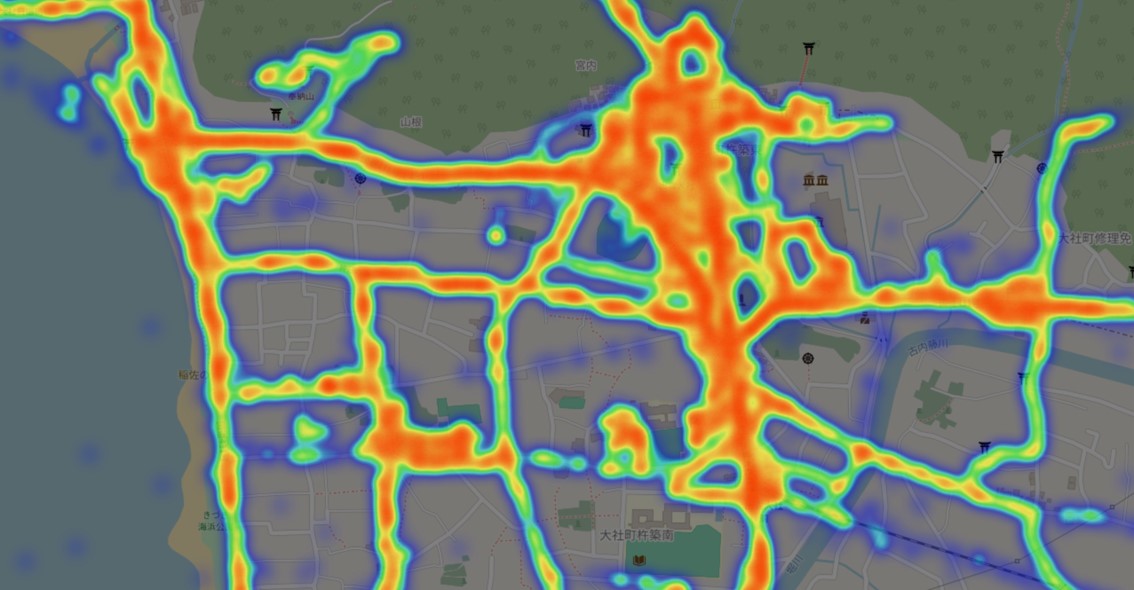
弊社で取集したデータはAI(機械学習)を用いて各種移動方法を自動で判別して記録しております。この技術は行動パターンから人物のペルソナ像を浮かび上がらせることができ、興味関心のあることや推定居住地を出すことができます。今回はそのデータから三陸鉄道駅周辺の滞在を見てみました。
※施設名などフォーカスしていない細かい滞在が集中している場所は商業施設や会社などが集まっているスポットです。
盛駅

三陸鉄道起点となる盛駅は大船渡の玄関となる場所です。
駅周辺には商業施設や市役所、市民会館や病院など地域住民の方が訪れる場所での滞在が見られました。
釜石駅

『JR釜石線』の乗り換えに利用する駅のため、他の駅と比べ駅周辺での滞在が多く見られました。商業施設や宿泊施設もありますが、駅から離れたところにある「イオンタウン釜石」「釜石市民ホールTETTO」など大きい施設周辺でも滞在が多く見られました。
大槌駅

ひょうたん島の愛称で親しまれている「蓬莱島」に滞在が見られました。
地元住民だけでなく観光客も訪れるスポットのようです。
「ますと乃湯」の近くに「蓬莱島」という飲食店があり、この周辺も多くの人が立ち寄っているようです。
宮古駅

『JR山田線』の乗り換えに利用する駅であり、多くの滞在が見られました。
観光名所である「浄土ヶ浜」「青の洞窟」や、お刺身が食べられる休憩スポットとしても口コミで評判の「宮古市魚菜市場」、本州最東端の道の駅「みやこ」などがあり、地元住人だけでなく観光客も多く訪れる駅です。
普代駅

他の駅と比べると滞在が少ないですが、道の駅を併設しているため駅周辺と「普代浜園地キラウミ」に滞在が見られました。
堀内駅

ドラマのロケ地にも使用された駅ですが、駅周辺の観光スポットというよりは乗車中に車窓を楽しめる区間が魅力的なようです。「大沢橋梁」と「安家川橋梁」では景色がよく見えるように、日中帯は橋の上で列車が一時停車、または徐行します。
陸中野田駅

こちらも道の駅を併設している駅です。道の駅にあるソフトクリーム屋には野田村の海水を煮詰めて作る「のだ塩」と野田村産の食用菊が隠し味の「のだ塩ソフト」が有名で、観光の際はぜひとも食べてみたい一品です。駅から離れると、「野田村地域包括支援センター」や「野田村役場」で滞在が見られました。
久慈駅

リアス線の最北端に位置し、三陸鉄道終点となる久慈駅は、ドラマの舞台となった駅です。滞在データで見ると、駅周辺の他に「道の駅くじ」「岩手県立久慈病院」「ショッピングモール」で多くの滞在が見られました。ドラマの主人公が海女として潜っていた「小袖海岸」は県外からの訪問者もおり、聖地巡礼や観光スポットとして人気があるようです。
・各駅の滞在比率
今回フォーカスした各駅の滞在比率はこのような結果となりました。
どの駅も魅力的ですが、宮古駅は盛岡駅を繋ぐ乗り換え地点であり、観光スポットが多いことから特に滞在比率が高いようです。

4. 調査元データ
データは弊社アプリ「SilentLog」から匿名化されたものであり、推定情報に基づいています。
※データはあくまで弊社サービスで収集したもので、実際とは異なる場合がございます
<データ概要>
【調査対象期間】
2023/4/1 − 2024/3/31
【調査対象エリア】
・盛駅
・釜石駅
・大槌駅
・宮古駅
・普代駅
・堀内駅
・陸中野田駅
・久慈駅
【各駅の滞在者数】
2023/4/1 − 2024/3/31 にマップに表示された駅周辺の滞在者合計数を100とした時の比率
【結果まとめ】
・宮古駅をはじめとした、別路線への乗換駅での滞在が多い
・大沢橋梁と安家川橋梁の停車スポットで滞在が見られた
・観光客にも人気のスポットはやはり滞在が多く見られた
5. 今年で開業40周年を迎える三陸鉄道
公式サイトで紹介されている40周年キャンペーンの一部を紹介いたします。
三陸鉄道公式サイト:https://www.sanrikutetsudou.com/
・40歳限定!無料乗車キャンペーン
三陸鉄道40周年と同い年である40歳の方は、三陸鉄道リアス線全線を年1回限定で無料乗車できるキャンペーンです。切符の購入やご利用について各条件がございますのでご興味のある方は公式サイトから詳細をご覧ください。
・三陸鉄道開業40周年記念「ウニ列車」
40周年記念として、従来の「プレミアムランチ列車春号」をグレードアップさせ、新たに「ウニ列車」を運行するそうです。車内では「生うに丼」や「うに丼(蒸し)」などが提供され、美しい大自然の車窓を眺めながら列車の中で「生うに丼」を食べられるのは大変珍しく、特別な体験ができます。車内サービスには「アテンダントによる車内ガイド」「記念乗車証」「海女さん・三鉄社員なりきりフォトコーナーの設置」があります。
運転日は2024年5月18日から6月16日までの土休日(全10回)です。ご興味のある方は公式サイトから詳細をご確認ください。
・三陸鉄道開業40周年記念400円きっぷ
2024年度内に4回「三陸鉄道開業40周年記念400円きっぷ」を発売し、全長163kmの三陸鉄道全線が1日400円で乗り放題できるキャンペーンを実施しています。(キャンペーン実施当日1日限り有効)第1回目は 2024年4月13日(土)に実施されました。盛駅〜久慈駅は3,780円なのでとてもお得に三陸鉄道を楽しむことができます。
その他の3回は、9月実施予定の大船渡派出所「3鉄まつり」、10月実施予定の「宮古車両基地まつり」、11月実施予定の久慈派出所「秋のさんてつまつり」開催日のようです。きっぷの発売日は決定次第お知らせするようなので、三陸鉄道開業40周年記念特設ページをご確認ください(https://www.sanrikutetsudou.com/40th/)
三陸鉄道に乗車の際は「さんてつアプリ」を利用すると、駅ごとのおすすめスポットや列車の現在地を確認することができ、ポイントまで貯まるのでお得に利用することができます。詳細はアプリページをご覧ください。
さんてつアプリ:https://santetsu.rei-frontier.jp/
6. 今回のまとめと今後の展望
今年で開業40周年を迎える三陸鉄道の魅力に迫りました。
また、三陸鉄道の社員と地域住民のボランティアによって発行されている「駅-1(エキイチ)グルメ」では、飲食店を調査し、お店や料理を紹介しているので、こちらの冊子を片手に三陸の旅をすれば、さらに楽しむことができそうですね。
太平洋を一望できる場所や、新鮮な海鮮をいただきながら自然を堪能できる三陸エリアは、心地よく観光することができそうです。季節ごとにイベント列車が走り、地元住人に愛される三陸鉄道ですが、観光客にも愛される魅力をお伝えしてまいりました。私も三陸鉄道に乗車する際はウニ丼をいただきながら太平洋をのんびり眺めたいと思います。
弊社独自で収集した人流データを使って、新しい観光施設開業前後の来場者数の変化や属性を分析することで、企業誘致や新しい施設の効果測定など様々な施策に活用することができます。
今後も位置情報データを活用して、各種施設の利用傾向や地域の特性を探ることで、より効果的な施策やサービスの提供に努めていきます。レイ・フロンティアは、最新の技術を駆使し、地域社会と連携しながら、より良い未来の構築に取り組んで参ります。
お知らせ
毎日の振り返る楽しさを「プラス」するアプリSilentLogの公式サイトはこちらです。
インストールサイトはこちらです。
【Android版】
【 iPhone版】
レイ・フロンティアの公式サイトはこちらです。
個人向けスマートフォンアプリの開発運用、及び、法人向けに独自の移動データの収集・推定技術を強みとした、サービスの企画提案コンサルティング、アプリケーションデザイン・開発、運用中のカスタマーサクセス支援(開発・技術支援等)を行っております。
レイ・フロンティアでは共に未来を切り開く仲間を募集しております。ご興味がある方はお気軽にお問い合わせください。
【各種SNS】
Twitter:https://twitter.com/reifrontier/
Youtube:https://www.youtube.com/user/reifrontier/
Instagram:https://www.instagram.com/reifrontier/
【本件に関するお問い合わせ】
お手数ですが、弊社お問い合わせページよりご連絡ください。



























 対象ユーザー全体では50代が多かったですが、寄り道ユーザーの結果から20代、30代、40代の寄り道率が高いです。70代は少ないサンプルでしたが、調査対象者がアクティブな高齢者だった可能性を推測します。
対象ユーザー全体では50代が多かったですが、寄り道ユーザーの結果から20代、30代、40代の寄り道率が高いです。70代は少ないサンプルでしたが、調査対象者がアクティブな高齢者だった可能性を推測します。


 日曜は「教会・寺院」「ホームセンター」「観光地」がランクインしています。
日曜は「教会・寺院」「ホームセンター」「観光地」がランクインしています。







 ウォーキングと徒歩の速さに地域差があることがわかります。
ウォーキングと徒歩の速さに地域差があることがわかります。
 年代別と同様にこちらもウォーキングと徒歩を 30分を境に分けているのでウォーキングと徒歩の距離に差が出ています。
年代別と同様にこちらもウォーキングと徒歩を 30分を境に分けているのでウォーキングと徒歩の距離に差が出ています。











 群馬県に位置するたんばらスキーパークおよび丸沼高原スキー場において、初雪観測前後の来場者数に差異が見られました。特に初雪観測後の1月において来場者数が増加しています。この傾向は、冬季スポーツのシーズン到来に伴い、スキーヤーやスノーボーダーが増加する傾向があることがわかります。
群馬県に位置するたんばらスキーパークおよび丸沼高原スキー場において、初雪観測前後の来場者数に差異が見られました。特に初雪観測後の1月において来場者数が増加しています。この傾向は、冬季スポーツのシーズン到来に伴い、スキーヤーやスノーボーダーが増加する傾向があることがわかります。