レイ・フロンティア株式会社 機械学習エンジニアの野島です。
レイ・フロンティア株式会社では、SilentLogを介して得られる行動情報を蓄積し、分析しています。
今回は「GPSデータをクラスタリングしてみた」の続きで、さらなる深掘り分析を行いましたので、その結果をまとめます。
目次
分析の概要
今回は主に 「グラフ」を用いて分析しました。
グラフについて
グラフとは、頂点の集合と、その間の接続関係を表す枝の集合で構成されています。
\(G=(V,E)\) で表現され、\(V\) は頂点の集合、\(E\) は枝の集合です。
図で表すと下図のようになります。
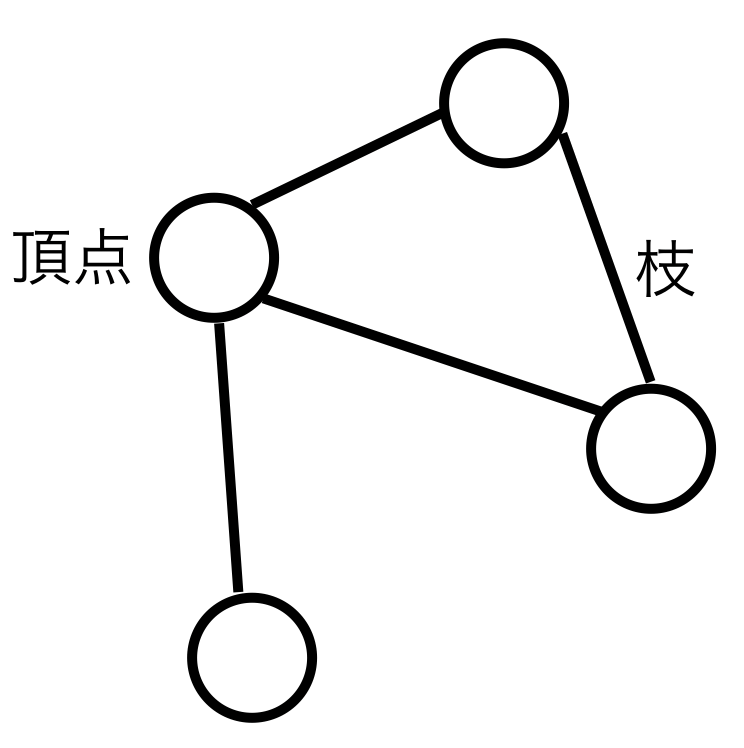
本分析で使用するグラフに関する用語は、グラフに関する用語の詳細説明で説明しています。
分析の手順
分析の大まかな流れは、下記のようになります。
1. GPSデータをクラスタリングする
前回の記事「GPSデータをクラスタリングしてみた」の方法でクラスタリングします。
2. 1.で得られたクラスタをグラフの頂点にする
3. 頂点間に枝を設定する
枝の設定(有向枝、無向枝、重み等)は、分析の種類によって異なります。
4. 構成したグラフに対し、グラフアルゴリズムを適用する
本分析で使用するグラフアルゴリズムについては、グラフアルゴリズムの詳細説明で説明しています。
分析1 : 滞在地点クラスタ間の人の流れを分析
分析の目的
滞在地点のクラスタに対し、どのクラスタ間の人の流れが多いかを分析する
分析の手順
1. 滞在地点をクラスタリングする
2. 得られたクラスタをグラフの頂点に設定
3. クラスタ間の人の流れをグラフの枝に設定
クラスタ間を移動した人数を計算し、移動した人が存在すれば枝を設定し、その人数を枝の重みに設定する。移動した人が存在しなければ枝を設定しない。
4. 得られたグラフに対し、最大全域木を求める
5. 得られた最大全域木の枝の頂点間が人の流れが多い経路とする
分析結果1
2019年10連休(4/27~5/6)に、東京スカイツリーに滞在があるSilentLogユーザーに対する結果です。
得られた最大全域木を図で表すと下図のようになります。
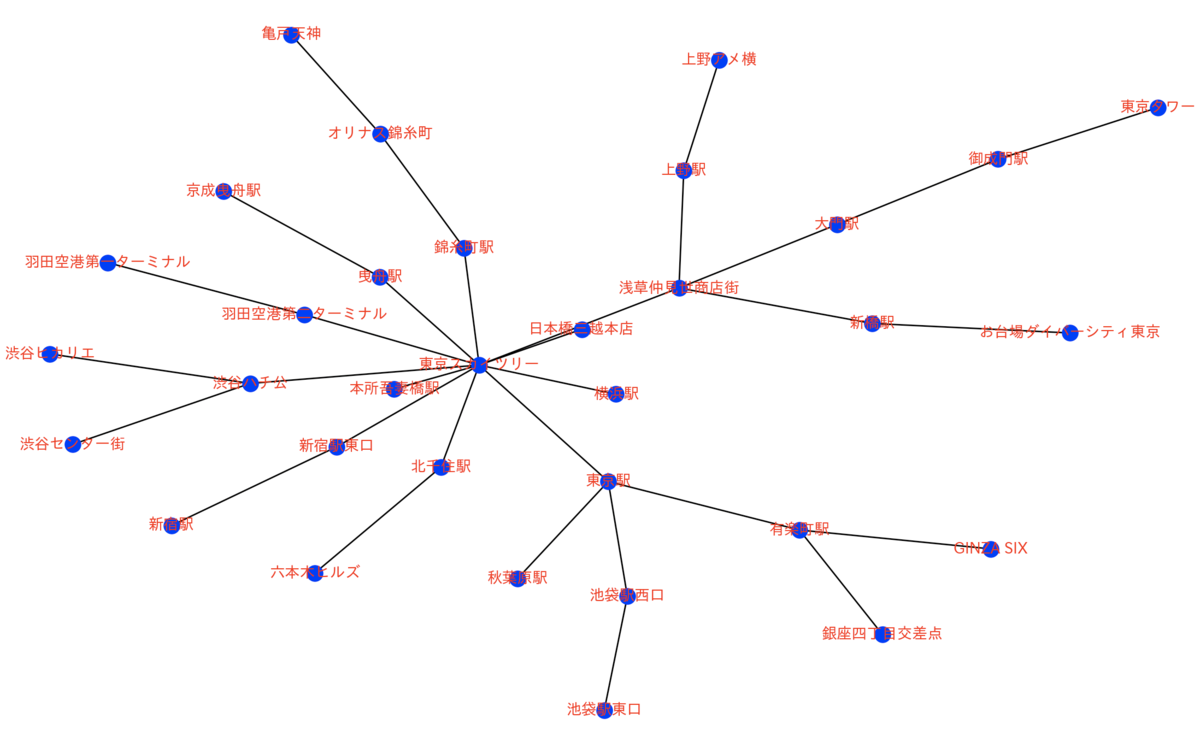
主な経路を抽出すると、下記のようになります。
①東京スカイツリー から 上野アメ横
東京スカイツリー \( \to \) 浅草仲見世商店街 \( \to \) 上野駅 \( \to \) 上野アメ横
②東京スカイツリー から 東京タワー
東京スカイツリー \( \to \) 浅草仲見世商店街 \( \to \) 大門駅 \( \to \) 御成門駅 \( \to \) 東京タワー
③東京スカイツリー から 六本木ヒルズ
東京スカイツリー \( \to \) 北千住駅 \( \to \) 六本木ヒルズ
④東京スカイツリー から お台場ダイバーシティ東京
東京スカイツリー \( \to \) 浅草仲見世商店街 \( \to \) 新橋駅 \( \to \) お台場ダイバーシティ東京
⑤東京スカイツリー から 亀戸天神
東京スカイツリー \( \to \) 錦糸町駅 \( \to \) オリナス錦糸町 \( \to \) 亀戸天神
連休なので、東京スカイツリーを訪れた人は、他の東京の観光地も併せて訪れていることが分かりました。
分析結果2
2019年10連休(4/27~5/6)に、京都駅に滞在があるSilentLogユーザーに対する結果です。クラスタの場所は京都市内に限定しました。
得られた最大全域木を図で表すと下図のようになります。
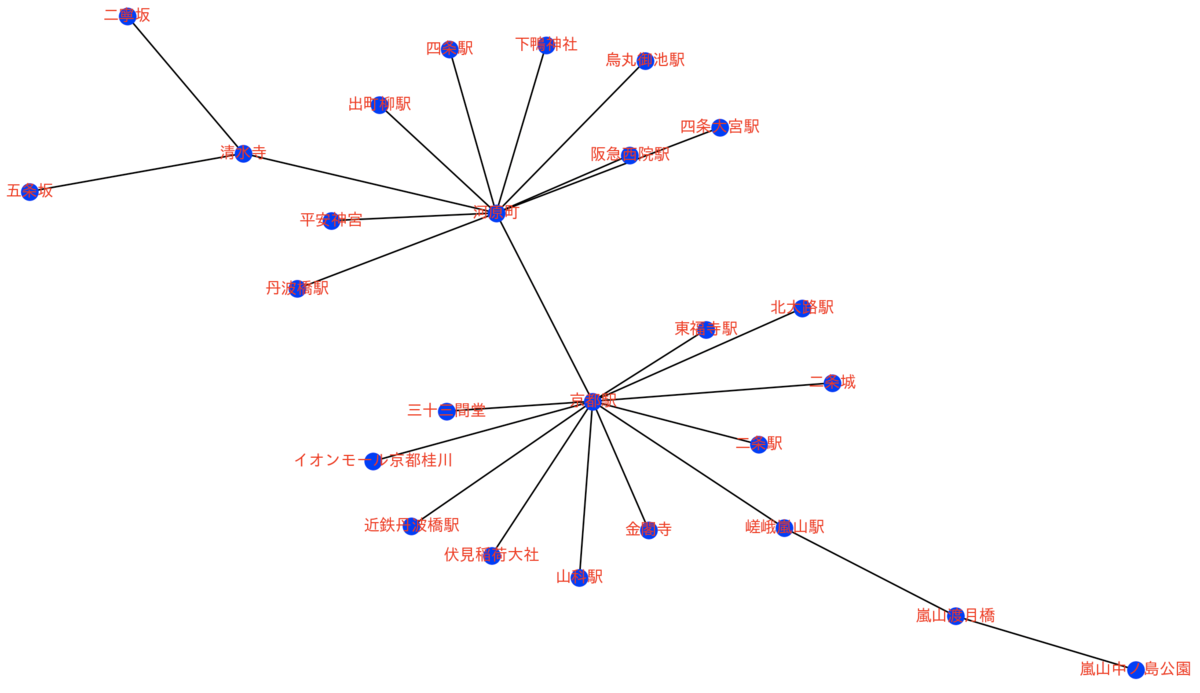
経路の起点として、京都駅と河原町の2地点存在することが分かりました。
京都駅からの主な目的地は、
三十三間堂、伏見稲荷大社、金閣寺、嵐山、二条城
となっていました。
河原町からの主な目的地は、
平安神宮、清水寺、下鴨神社
となっていました。
分析2:滞在地点クラスタ間での通過駅の分析
分析の目的
分析1で得られた経路(最大全域木)を更に分析し、通過駅を抽出する
分析の手順
(手順1 ~ 4は分析1と同じです。)
1. 滞在地点をクラスタリングする
2. 得られたクラスタをグラフの頂点に設定
3. クラスタ間の人の流れをグラフの枝に設定
クラスタ間を移動した人の人数を数え、移動した人が存在すれば枝を設定し、人数を枝の重みに設定する。移動した人が存在しなければ枝を設定しない。
4. 得られたグラフに対し、最大全域木を求める
5. 最大全域木で定義された枝に対し、そこを経由したユーザーを取得
6. 取得したユーザーに対し、移動経路と駅の地点との比較を行い、通過した駅を抽出する
7. 通過した駅をグラフの頂点、通過した駅間を時系列で順番に有向枝を設定し、グラフを構成する
8. 求めたグラフにおいて最短パスを求める
9. 抽出した最短パスから経由した駅、使用した路線が抽出できる
分析結果
2019年10連休(4/27~5/6)に、東京スカイツリーに滞在があるSilentLogユーザーに対する結果です。
通過した駅から利用した路線を抽出した主な結果は下記になります。
(1) 東京スカイツリー から 六本木ヒルズの経路
分析1で抽出した経路の結果は、
東京スカイツリー \( \to \) 北千住駅 \( \to \) 六本木ヒルズ
でした。
通過した駅から抽出した利用路線の結果は、
東京スカイツリー から 北千住駅 までは、東武伊勢崎線
北千住駅 から 六本木ヒルズ までは、東京メトロ日比谷線
でした。
(2) 東京スカイツリー から お台場ダイバーシティ東京
分析1で抽出した経路の結果は、
東京スカイツリー \( \to \) 浅草仲見世商店街 \( \to \) 新橋駅 \( \to \) お台場ダイバーシティ東京
でした。
通過した駅から抽出した利用路線の結果は、
東京スカイツリー から 浅草仲見世商店街 までは、東武伊勢崎線
浅草仲見世商店街 から 新橋駅 までは、都営浅草線
新橋駅 から お台場ダイバーシティ東京 までは、ゆりかもめ
でした。
まとめ
今回は、グラフ理論を用いて分析を行いました。
グラフにより行動情報をモデル化し、グラフアルゴリズムを適用することにより、経路や通過駅を抽出しました。
今回の記事は以上となります。
今後も本ブログを通して発信していきます。
詳細説明
グラフに関する用語
本分析で使用したグラフに関する用語について説明します。
有向枝
向きの情報を付加した枝です。
例えば、頂点Aから頂点Bに移動したことを表現する場合に、頂点Aから頂点Bに矢印の有向枝を設定します。
無向枝
向きの情報を付加せず、接続情報のみの枝です。
無向グラフ
無向枝のみのグラフです。
有向グラフ
有向枝のみのグラフです。
パス(経路)
ある頂点からある頂点に至るまでの経由した頂点の列です。
例)下図において、頂点Aから頂点Dまでのパスは、[A, B, D]と表せる。
連結グラフ
任意の2頂点間にパスが存在するグラフです。
閉路
始点と終点が同一のパスです。
例)下図においては、パス[A, B, C, A]が閉路となります。
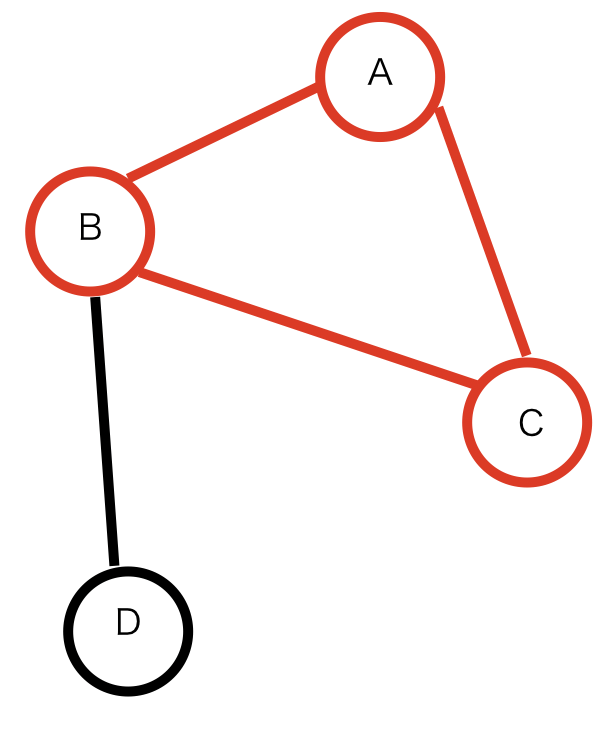
木
閉路の無い連結グラフです。
枝の重み
枝に数値を設定でき、コスト、距離などを設定します。
重みが設定されているグラフを重み付きグラフと言います。
全域木
グラフの全ての頂点とそのグラフを構成する辺の一部分のみで構成される木です。
その他
その他、グラフ理論に関する詳細は、下記をご参照ください。
グラフアルゴリズム
ここでは、本分析で使用したグラフアルゴリズムについて説明します。
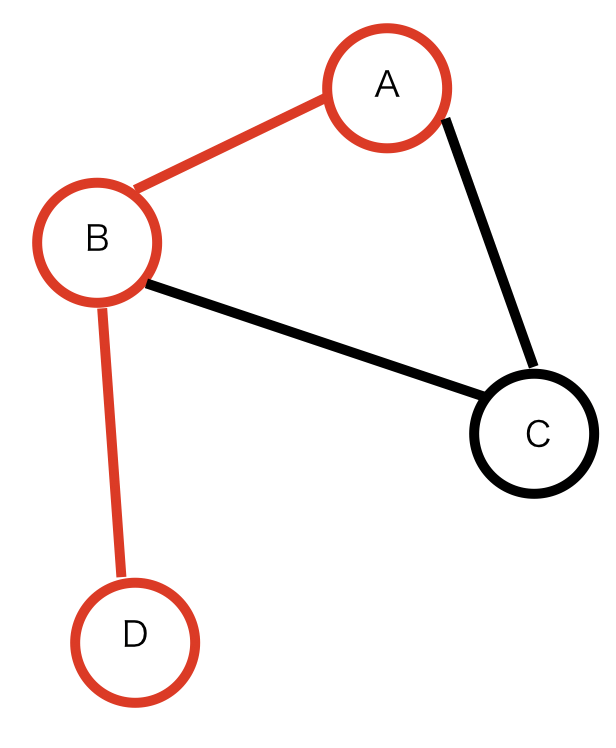
最大全域木
最大全域木とは、各辺に重みがある場合、最大の総和コストで構成される全域木です。
最小全域木もありますが、これは、最小の総和コストで構成される全域木のことです。
最大全域木も最小全域木も同じ方法で求めることができます。
例)下図の場合、赤線の全域木が最大全域木となります。
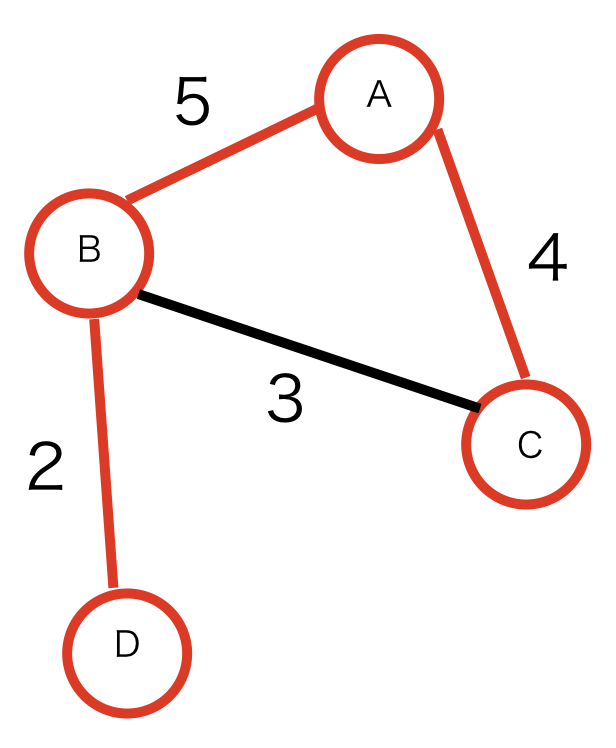
最大全域木を求める代表的なアルゴリズムとしては、「クラスカル法」と「プリム法」が存在します。
・クラスカル法
クラスカル法については以下を参照してください。下記は「最小全域木」を求める方法が紹介されていますが、「最小」を「最大」に読み替えていただければ、最大全域木を求めることができます。
・プリム法
プリム法については以下を参照してください。こちらも「最小全域木」を求める方法ですので、「最小」を「最大」に読み替えていただければ、最大全域木を求めることができます。
最短パス
最短パスとは、重み付きグラフにおける2頂点間のパスの中で、 重み総和が最小なパスです。
例)下図の場合、A から D の最短パスは、[A, C, B, D]となります。
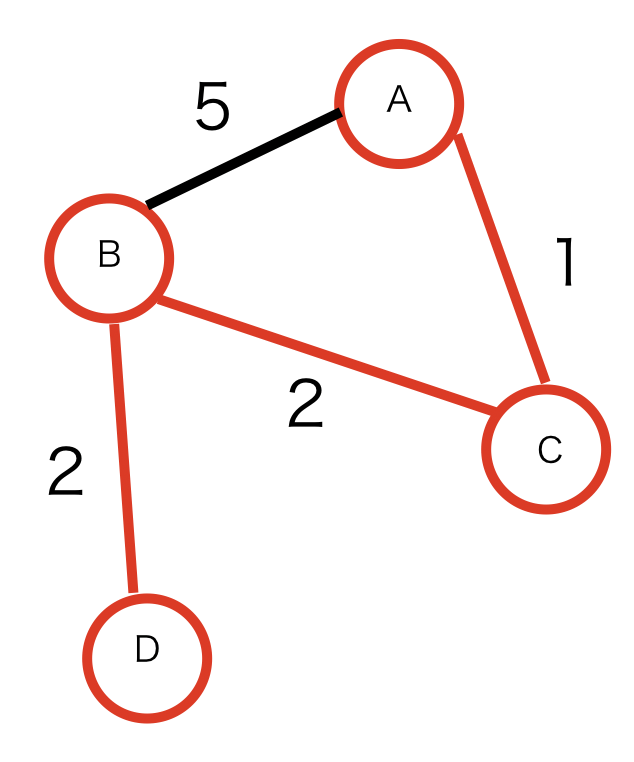
最短パスを求める代表的なアルゴリズムとしては、「ダイクストラ法」が存在します。
最短パスに関する詳細は、下記をご参照ください。